Fórmulas de cálculo
Retângulo
Retângulo com área lw.
A mais simples fórmula de cálculo de uma área é a do retângulo. Dado um retângulo com base l e altura w, a sua área é:
 (área do retângulo)[3]
(área do retângulo)[3]
Ou seja, a área do retângulo é obtida multiplicando a largura pela altura. Um caso particular é a área do quadrado; sendo l o comprimento do seu lado, a sua área é:
 (área do quadrado)
(área do quadrado)
A fórmula para a área do retângulo decorre diretamente das propriedades básicas da área, e por vezes é tomada como uma definição ou axioma. Tendo a geometria sido desenvolvida antes da aritmética, o conceito de área pode ser usado para definir amultiplicação de números reais.
Dissecção de um paralelogramo.
[editar]Fórmulas por dissecção
A maioria das outras fórmulas simples para o cálculo da área seguem o método da dissecção. Como o nome indica, este método envolve seccionar a figura em partes mais simples, calcular a área de cada uma dessas partes, que somadas resultarão na área da figura original.
Por exemplo, um paralelogramo pode ser dividido num trapezóide e numtriângulo retângulo, como ilustrado pela figura da esquerda. Se movermos o triângulo para o outro lado do trapezóide, o resultado é um retângulo. A conclusão é que a área do paralelogramo é igual à do retângulo:
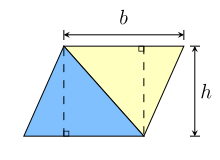
Dois triângulos iguais.
 (área do paralelogramo)
(área do paralelogramo)
O mesmo paralelogramo pode ser dividido em dois triângulos congruentes através de um corte na diagonal, como mostrado na figura da direita:
 (área do triângulo)
(área do triângulo)
É possível fazer raciocínios semelhantes para obter fórmulas para as áreas do trapezóide, do losango e de outros polígonos mais complicados.
Área de outros polígonos
Área do trapézio:
 (B = base maior; b = base menor; h = altura)[4]
(B = base maior; b = base menor; h = altura)[4]
Área do losango:
 (D = diagonal maior; d = diagonal menor)
(D = diagonal maior; d = diagonal menor)
Área de qualquer polígono regular:
Dividindo o círculo em setores que podem ser rearranjados num paralelogramo aproximado.
Círculo
A área de um círculo também pode ser calculada através do método de dissecção. Dado um círculo com raio  é possível dividi-lo em setores. Cada setor tem uma forma aproximadamente triangular, e os setores podem ser rearranjados para formar uma figura próxima de um paralelogramo. A altura do paralelogramo é
é possível dividi-lo em setores. Cada setor tem uma forma aproximadamente triangular, e os setores podem ser rearranjados para formar uma figura próxima de um paralelogramo. A altura do paralelogramo é  e a largura é metade dacircunferência do círculo, ou seja,
e a largura é metade dacircunferência do círculo, ou seja,  . Resulta que a área do círculo é
. Resulta que a área do círculo é  , ou seja,
, ou seja,  :
:
 (área do círculo; r = raio)
(área do círculo; r = raio)
Embora a dissecação usada na fórmula seja aproximada, o erro torna-se cada vez mais pequeno à medida que usamos setores cada vez mais pequenos. O limite da área quando o tamanho dos setores tendo para zero é exatamente  , que corresponde à área do círculo.
, que corresponde à área do círculo.
Este raciocínio é uma aplicação simples dos conceitos do cálculo. No passado, o método da exaustão foi usado de forma semelhante para encontrar a área do círculo, sendo reconhecido como um precursor docálculo integral. Usando os métodos modernos, a área do círculo pode ser calculada usando um integral:
Área de uma superfície
Arquimedes relacionou a área e volume da esfera com o cilindro.
A maioria das fórmulas para o cálculo da área de uma superfície pode ser obtida cortando e endireitando a superfície. Por exemplo, a superfície de um cilindro pode ser cortada e estendida formando um retângulo. Da mesma forma, a superfície de um cone pode ser cortada e endireitada num setor de um círculo, para permitir o cálculo da sua área.
O cálculo da área da superfície de uma esfera é mais complexo, pois a curvatura da superfície dificulta a sua projeção num plano direito. Isso acontece com sólidos com curvatura gaussiana diferente de zero. O primeiro a obter uma fórmula para o cálculo da área de uma esfera foiArquimedes na sua obra Sobre a Esfera e o Cilindro. Provou que a área e volume da esfera é exatamente 2/3 da área e volume do cilindro que a envolve. Tal como acontece com a área do círculo, a fórmula para a área da esfera resulta de métodos similares aos do cálculo.
Á área de uma esfera com raio  é:
é:
 (área da esfera)
(área da esfera)
Lista de fórmulas
Fórmulas comummente usadas para o cálculo da áreaFigura
Formula
Variáveis
Triângulo equilátero
 é comprimento de um lado do triângulo.
é comprimento de um lado do triângulo.
Triângulo
 é metade do perímetro,
é metade do perímetro,  ,
,  e
e  é o comprimento de cada um dos lados.
é o comprimento de cada um dos lados.
Triângulo
 e
e  são quaisquer dois lados, e
são quaisquer dois lados, e  é o ângulo entre eles.
é o ângulo entre eles.
Triângulo
 e
e 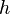 são a base e altura (medida perpendicularmente à base), respetivamente.
são a base e altura (medida perpendicularmente à base), respetivamente.
Quadrado
 é o comprimendo de um dos lados do quadrado.
é o comprimendo de um dos lados do quadrado.
Retângulo
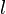 e
e  são o comprimento de cada um dos lados do retângulo.
são o comprimento de cada um dos lados do retângulo.
Losango
 e
e  são o comprimento de cada uma das diagonais do losango.
são o comprimento de cada uma das diagonais do losango.
Paralelogramo
 é o comprimento da base e
é o comprimento da base e 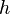 é a altura medida na perpendicular.
é a altura medida na perpendicular.
Trapezóide
 e
e  são os lados paralelos e
são os lados paralelos e 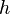 a distância (altura) entre os lados paralelos.
a distância (altura) entre os lados paralelos.
Hexágono regular
 é o comprimento de um dos lados do hexágono.
é o comprimento de um dos lados do hexágono.
Octógono regular
 é o comprimento de um dos lados do octógono
é o comprimento de um dos lados do octógono
Polígono regular
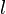 é o comprimento de um dos lados e
é o comprimento de um dos lados e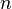 o número de lados.
o número de lados.
Polígono regular
 é o raio do círculo circunscrevente,
é o raio do círculo circunscrevente,  o raio do círculo interior, e
o raio do círculo interior, e 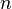 é o número de lados.
é o número de lados.
Polígono regular
 é o apótema (raio do círculo interior ao polígono) e
é o apótema (raio do círculo interior ao polígono) e  é o perímetro do polígono.
é o perímetro do polígono.
Círculo
 é o raio e
é o raio e 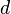 o diâmetro.
o diâmetro.
Setor circular
 e
e  são, respetivamente, o raio e ângulo (em radianos).
são, respetivamente, o raio e ângulo (em radianos).
Elipse
 e
e  são o semieixo maior esemieixo menor, respetivamente.
são o semieixo maior esemieixo menor, respetivamente.
Área total da superfície do cilindro
 e
e 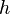 são o raio e altura do cilindro.
são o raio e altura do cilindro.
Superfície lateral do cilindro
 e
e 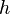 são o raio e altura do cilindro.
são o raio e altura do cilindro.
Superfície total docone
 e
e 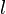 são o raio e a distância do vértice ao círculo base, respetivamente.
são o raio e a distância do vértice ao círculo base, respetivamente.
Superfície total daesfera
 e
e 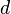 são o raio e o diâmetro, respetivamente.
são o raio e o diâmetro, respetivamente.
Superfície total dapirâmide
 é a área da base,
é a área da base,  o perímetro da base e
o perímetro da base e  a distância do vértice aos cantos da base.
a distância do vértice aos cantos da base.


 (P =
(P = 


Nenhum comentário:
Postar um comentário